The Dynamism of Innovation.

Exploring how change, context, and purpose shape true innovation.

What does innovation mean to you? what did it mean in the past? and what does it mean now. Do you think this will also change?

These are questions I ask myself, and believe everyone should. Think on this often. One fascinating lesson from quantum physics is that the very act of observation changes what is being observed. It has led me to believe that nothing ever truly stays the same — not even artificial intelligence or innovation in Formula 1 engineering.

Simply put, innovation is the creation of a system that delivers significantly better performance in one or more areas—whether within or beyond established rules—and represents an idea that was previously unforeseen.

Within the boundaries of nature and physics, there’s only a finite range of innovations possible at any given time. Doing something different isn’t always innovative — but true innovation almost always requires doing something different.

When improving any engineering solution — MLOps included — it’s essential to ask: what’s the ultimate goal? Are we simply doing something different, or are we creating something truly innovative? Clarity on this, both for yourself and your stakeholders, is vital.

To create something truly innovative, we must study what has been done before—how the rules evolved, which perceived weaknesses might hide strengths, and, above all, what the real goal is. Are we aiming for a more reliable car? A faster one—on the straights, the corners, or both? A telemetry system with lower latency? Innovation demands a clear purpose, not just a scatter of efforts in different directions.

Each team must define what innovation means for them at any moment—based on their position on the grid, available resources, and end-of-season goals. In other words, start with purpose, then shape innovation around it. After the season, reflect on results and lessons learned to redefine that meaning, because innovation is fluid—dynamic, and ever-changing.

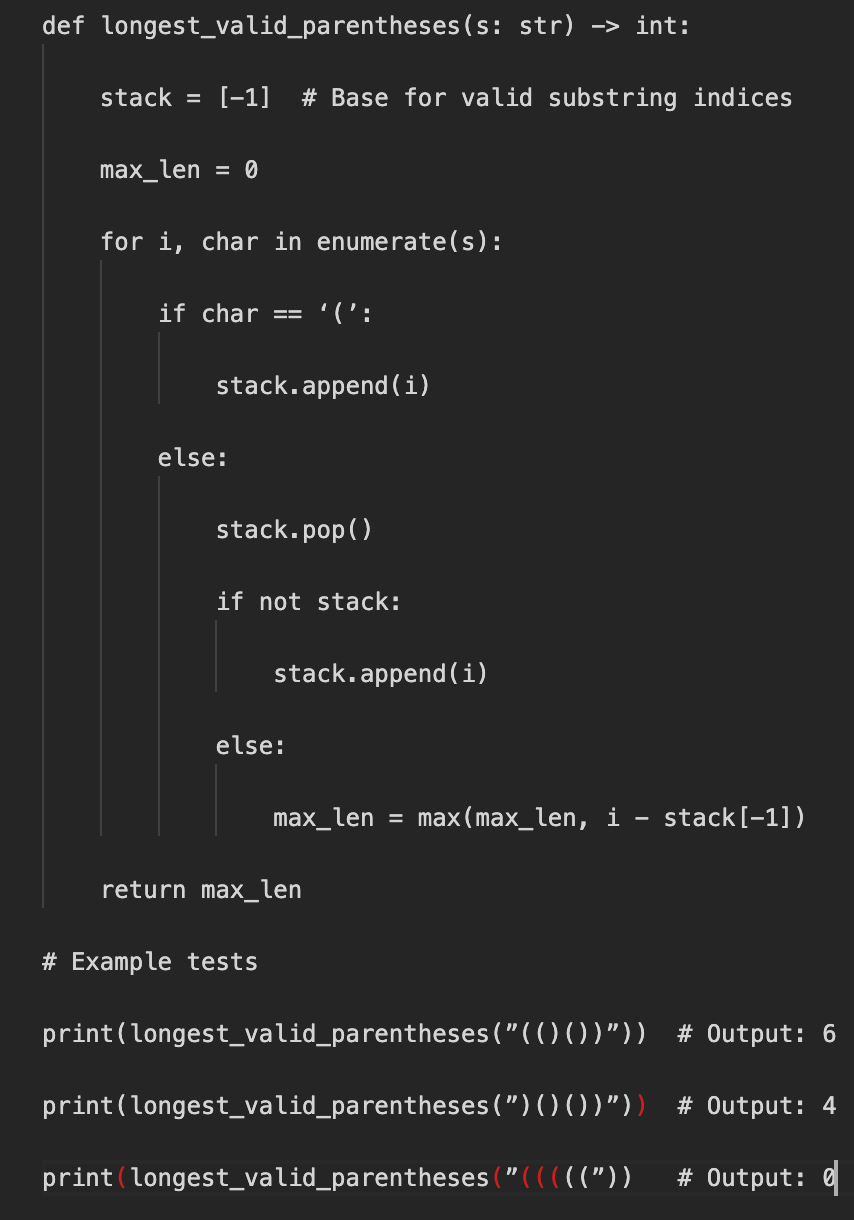
Coding Exercise

Longest Balanced Substring of Brackets - Medium Difficulty

You are given a string s consisting only of the characters ‘(’ and ‘)’.
Your task is to find the length of the longest balanced substring of parentheses.

A substring is considered balanced if every opening parenthesis ‘(’ has a corresponding closing parenthesis ‘)’ in the correct order.

Constraints:

• 1 <= len(s) <= 10^5

• s contains only ‘(’ and ‘)’.

Solution

Explanation:

• Use a stack to track indices of ‘(’ characters.

• Push -1 initially to handle edge cases.

• Every time a ‘)’ matches a ‘(’, compute the current valid substring length.

• Update max_len with the longest length seen so far.